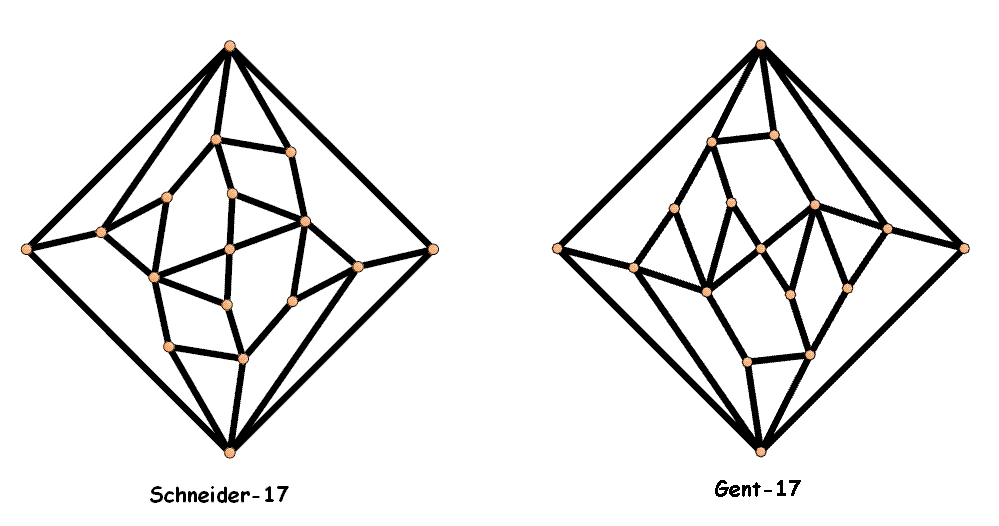Der Schneider von Gent

Brettspiel von Ingo Althöfer,
Copyright März 2013

"Der Schneider von Gent" ist ein asymmetrisches Spiel für zwei Personen. Die Idee dazu kam mir, als zwei verschiedene alternierende planare Graphen mit 17 Knoten und 17 Flächen gefunden worden waren: einer (der "Schneider-17") von Frank Schneider schon im Frühjahr 2008, der andere ("Ghent-17") durch die Gruppe von Professor Gunnar Brinkmann an der Universität von Gent Anfang 2013.


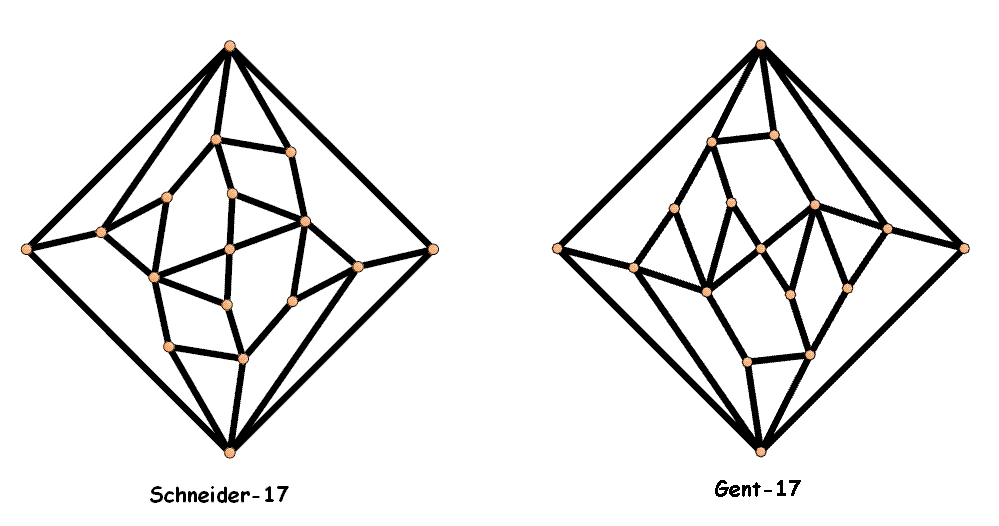
Die "Gent-Gruppe" bewies auch mit vollständiger Enumeration, dass dieses die beiden einzigen alternierenden planaren Graphen mit 17 Knoten sind. Ihre Computer-Läufe zeigten auch, dass es keine 3-zusammenhängenden alternierenden planaren Graphen mit weniger als 17 Knoten gibt.

Als Stadt war das belgische Gent über etliche Jahrhunderte berühmt für die Herstellung und den Handel von Tuchstoffen. "Schneider" ist der Familienname von Frank Schneider. Diese Querbeziehung - zusammen mit der Beobachtung, dass planare Graphen passender Grösse schöne Spielbretter abgeben - liess mich über ein zugehöriges Brettspiel nachdenken.


"Der Schneider von Gent" kann entweder auf dem "Schneider-17" oder auf dem "Ghent-17" gespielt werden. Zu Hause habe ich ein laminiertes Brett, wo auf der einen Seite der Schneider-17 drauf ist, und auf der Rückseite der Ghent-17. Je nach Stimmung wird auf diesem ode jenem Brett gespielt.

Spielmaterial
Das Spielbrett ist entweder der Ghent-17 oder der Schneider-17, gezeichnet als planarer Graph mit einem Viereck als Aussenfläche. Ein Fingerhut, etwa 50 Streichhölzer, und 16 Knöpfe.

Die zwei Spieler sind:
(S) Der Schneider. Seine einzige aktive Figur ist der Fingerhut. Der Schneider nutzt die Streichhölzer, um die Kanten zu markieren, über die der Fingerhut schon gelaufen ist.
(K) Herr Knöpfle. Seine Figuren sind die 16 Knöpfe.

Vorbereitung für eine Partie
In jede der 16 inneren Flächen des Spielbretts wird ein Knopf gelegt. (Die Aussenfläche hat im Spiel keine Rolle.) Ein Knopf in einer Fläche heisst frei, ein Knopf auf einem Knoten zählt als gefangen und kann nicht mehr bewegt werden.

Verlauf des Spiels
Die Spieler ziehen abwechselnd. Vor dem ersten normalen Zug wählt Herr Knöpfle einen Knoten als Startknoten für den Fingerhut des Gegners aus. Danach ist die Zugreihenfolge strikt alternierend, beginnend mit dem Schneider (also S-K-S-K-S-...).

In jedem Zug des Schneiders wandert der Fingerhut von seinem aktuellen Knoten aus über eine offene Kante zu einem Nachbarknoten. Es ist wichtig, dass auf dem Nachbarknoten noch kein Knopf liegt und auf der benutzten Kante noch kein Streichholz. Am Ende des Zuges wird die benutzte Kante durch längs liegende Streichhölzer markiert, entweder durch ein einzelnes (bei einer kurzen Kante) oder mehrere. Es soll ein bisschen so aussehen wie eine saubere Schneider-Naht. Jetzt kommt der Belohnungsteil des Zuges: Wenn in mindestens einer der beiden Nachbarflächen der benutzten Kante noch ein Knopf liegt, darf der Schneider solch einen nehmen und auf den Startknoten seines aktuellen Zuges legen. Jedoch: Wenn er will, darf der Schneider auch auf das Umlegen eines solchen Knopfes verzichten. Auf jeden Fall muss der Schneider die benutzte Kante mit Streichhölzern markieren. Der Graph hat 32 Kanten, so ist die Partie sp&aul;testens nach 32 Zügen des Schneiders zu Ende. (In der Praxis wird eine Partie selten länger dauern als 20 Zugpaare.)

Herr Knöpfle hat in jedem seiner Züge die Wahl: Entweder macht er einfach nichts. Oder er bewegt einen seiner freien Knöpfe über eine offene Kante in eine leere Nachbarfacette. (Noch mal zur Klarheit: die Aussenfläche ist nicht Teil des Spiels.)

Durch seine gelegten Nähte schafft der Schneider nach und nach ein Netz, was die Beweglichkeit seines Fingerhutes und auch die der gegnerischen Knöpfe einschränkt.

Auszählen am Spielende
Die Partie endet, wenn der Schneider keine zulässigen Züge mehr hat. Oft erkennt man schon mehrere Züge vor dem formalen Ende, dass der Schneider keine weiteren Knöpfe gefangen nehmen kann. Wenn beide Spieler das so sehen, kann die Partie schon an der Stelle abgebrochen werden und das Auszählen beginnen. Das Zählen funktioniert so: Für jeden gefangenen Knopf bekommt der Schneider so viel Punkte, wie aus dem zugehörigen Knoten Kanten herausgehen. Diese Punkte werden aufaddiert. Es macht also für den Schneider Sinn, Gefangene vor allem auf Knoten mit vielen Kanten zu machen.

Zwischen zwei Personen A und B werden zwei Partien wie oben beschrieben ausgespielt. In der ersten ist Spieler A der Schneider und B Herr Knöpfle. In Partie 2 sind die Rollen vertauscht. Gesamtsieger ist, wer als Schneider mehr Punkte geholt hat. Im Fall von Punktegleichheit zählt als "kleiner Sieger", wer in der ersten Partie der Schneider war.

Das Spiel ist so kompliziert, dass es nicht "einfach" mit Computerhilfe durchgerechnet werden kann.

Siehe auch die Seite zum Brettspiel Karls Rennen.

Hier sind ein paar Fotos aus einer Beispielpartie.


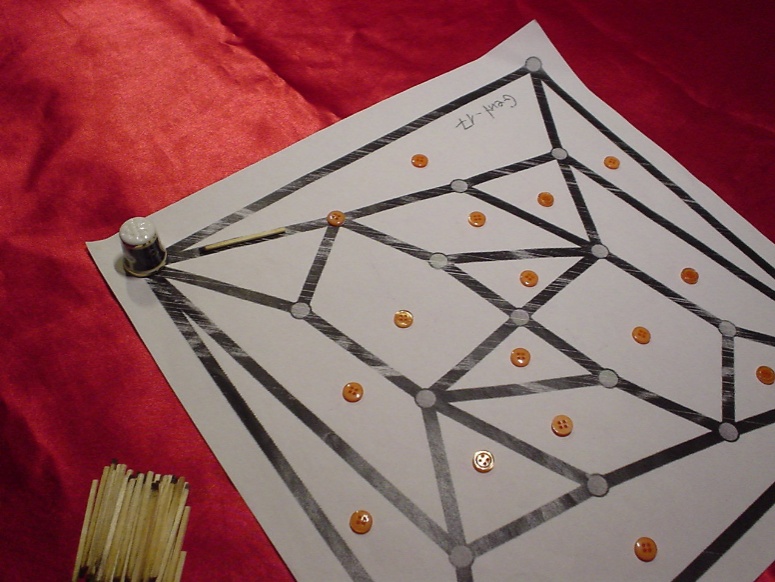
Stellung nach dem ersten normalen Zug des Schneiders. Das Streichholz zeigt, von wo der Fingerhut zum Eckknoten wanderte.


Nach dem ersten Zug von Herrn Knöpfle. Er hat tatsächlich einen Knopf umgelegt.



Stellung nach Zug 8 von Herrn Knöpfle.


Nach Zug 13 des Schneiders. Jetzt gibt es für den Fingerhut keinen zulässigen Zug mehr. So endet die Partie, und es wird ausgezählt.



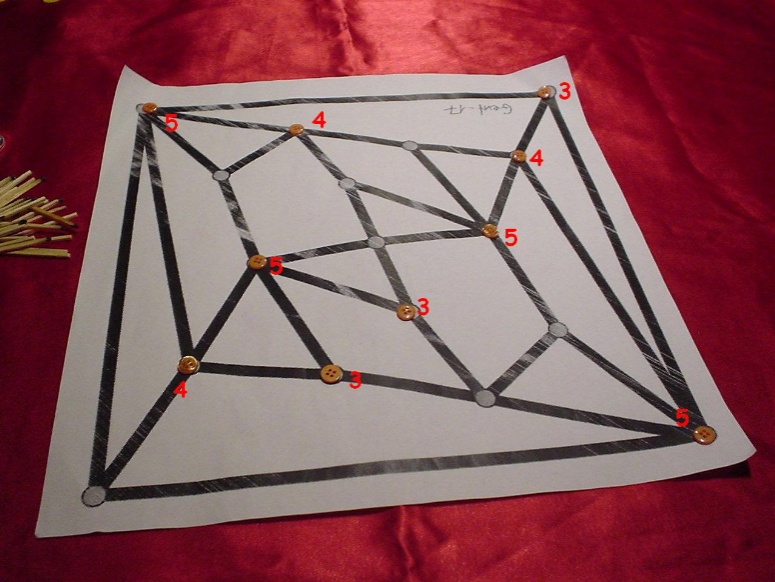
Hier sieht man die gefangenen Knöpfe zusammen mit den resultierenden Punkten für den Schneider. Sein Gesamtscore ist 41.

To the rules in English

Zurück zur Event-Seite des 3-Hirn-Verlags