Ingo Althöfer
Bei seinen Zeitgenossen war Gauss vor allem deshalb berühmt, weil er - damals als einziger! - die Bahndaten der ersten vier Asteroiden Ceres, Pallas, Juno und Vesta ordentlich berechnen konnte - und zwar so ordentlich, dass man die Kleinplaneten auch nach monatelanger beobachtungsloser Zeit wiederfand. Dafür wurde er 1807 mit einer Professur und dem Direktorposten der Göttinger Sternwarte belohnt.
Im Spiel geht es darum, einen zunächst völlig volatilen Asteroiden dingfest zu machen. Spieler Ceres hat nur den Asteroiden, einen 1er-Klotz in Braun. Spieler Gauss hat alle 18 blauen Klötze. Gezogen wird abwechselnd: Zunächst würfelt Gauss und setzt einen blauen Klotz passender Grösse auf irgendeinen freien Teil des Bretts. Danach darf Ceres mit seinem Asteroiden maximal so viele Schritte machen, wie der (noch liegende) Würfel Augen zeigt. Das Spiel endet entweder, wenn Ceres sich nicht mehr bewegen kann, oder wenn Jäger Gauss am Zug ist und keine Klötze mehr zum Einsetzen hat.

|
Reinhold Wittig
Dieses Spiel kann ohne Spielplan gespielt werden.
Spieler A stellt seinen ersten erwürfelten Klotz senkrecht hin oder legt ihn flach auf den Tisch. Spieler B stellt oder legt seinen Startklotz an, und zwar so, dass Flächenkontakt besteht. Jeder neue Klotz, der eingesetzt wird, kann senkrecht stehen oder waagerecht gelegt werden. Und er muss irgendwo Flächenkontakt zu einem anderen Klotz der gleichen Farbe haben. Spiel-Ziel: Der Gaussturm darf nicht höher werden als sieben Einheiten. Jede "Einheit" in Höhe Sieben zählt einen Punkt für den zugehörigen Spieler. Wer am Ende die meisten Punkte hat, gewinnt.
Zur Taktik: Die Bedingung des Flächenkontaktes nutzt man, um die Baumöglichkeiten des Gegenspielers dadurch zu reduzieren, dass man möglichst viele seiner Klötze zubaut.
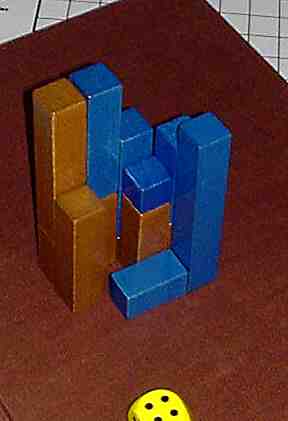
|
Ingo Althöfer
Auf Anregung von Gauss wurde 1831 der Physiker Wilhelm Weber an die Universität Göttingen berufen. Gauss und Weber waren zusammen sehr kreativ, vor allem bei der Erforschung des Erdmagnetismus.
Im Spiel stehen die beiden Klotzfarben blau und braun für die beiden magnetischen Pole. Gespielt wird auf dem kleinen Brett (10x10). Gezogen wird abwechselnd. Wer dran ist, würfelt und legt oder stellt dann einen Klotz passender Länge an eine freie Stelle des Spielbretts. Pole gleicher Farbe stossen sich ab; deshalb darf nicht blau an blau liegen und auch nicht braun an braun. Bei der Abrechnung bekommt jeder Spieler Strafpunkte: für jeden hochkant stehenden Klotz seiner Farbe dessen Höhe, für jeden aus dem Spiel gelegten Klotz die doppelte Höhe. Die kleinere Punktsumme gewinnt!

|
Reinhold Wittig
Beziehungen zu Gauss? Vielleicht macht man sich die Schwierigkeiten eines Umzugs damals klar, wie z.B. der von Braunschweig nach Göttingen, tagelang mit dem Ackerwagen.
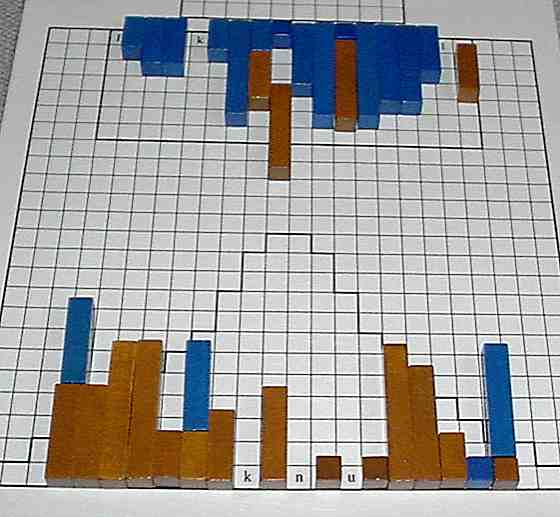
Grosser Plan, zwei sich gegenüber liegende Seiten sind die Start-Areale. Das Zielgebiet ist jeweils die gegenüberliegende Startseite des Gegenspielers. Der Spieler, der am Zug ist, bewegt einen Klotz. Dieser Klotz hat pro Zug eine Frei-Bewegung, ohne Richtungsänderung. Aber: Stösst er dabei gegen einen eigenen oder fremden Stein, erneuert sich seine Bewegungs-Energie, und er ändert seine Richtung.
Das reguläre Spiel endet, wenn ein Spieler seine freien Spielsteine so in seinem Zielgebiet hat, dass alle entweder den Spielfeldrand berühren oder direkt vor gefangenen Klötzen des Gegenspielers stehen. Nun werden die Züge gezählt, die der Gegner noch braucht, um auch seine Klötze in die endgültige Stellung zu bringen. Gefangene werden gegeneinander aufgerechnet. Die Gesamtbilanz ergibt den Gewinner. Dies braucht nicht derjenige zu sein, der zuerst fertig war!
|
Ingo Althöfer
Gewonnen hat, wer eine durchgehende Verbindung zwischen seinen beiden Brettseiten geschaffen hat: Blau von links nach rechts, Braun von oben nach unten. Solch eine Verbindung wird beileibe nicht geradlinig verlaufen und jedem Elektriker die Haare zu Berge stehen lassen! Das ist aber nicht schlimm.
Liegen irgendwann alle Klötze auf dem Brett, ohne dass eine Seitenverbindung erreicht wurde, tritt das Spiel in Phase 2 (Karin [Wittig]s Verlängerung). Statt einzusetzen, muss man eigene Klötze umlegen, auch wenn dabei schon bestehende Teil-Verbindungen zerstört werden. Ziel bleibt die Seitenverbindung.

|
Reinhold Wittig
Ein taktisches Spiel auf dem kleinen Brett, nach einem alten Spiel-Prinzip. Jeder hat einen Präsidenten (den Fünfer), drei C4-Steine, drei C3-Steine, drei C2-Steine sowie drei Einer als Hilfskräfte (die sich noch alles gegenüber den Längeren herausnehmen können!)
Die Hierarchie: Jeder Stein kann gleichlange oder kürzere Steine schlagen. Ein Fünfer kann also alle gegnerischen Steine schlagen, ein Dreier aber z.B. nur andere Dreier, Zweier und Einer. Die einzige Ausnahme stellen die Einer dar: Sie dürfen alle anderen schlagen! Es besteht Schlagzwang. Das Spiel-Ziel: Den gegnerischen Präsidenten abberufen, also schlagen. Dies geht nur durch den eigenen Präsidenten und die Hilfskräfte. (Die gegenständliche Benennung der Spielklötze bezieht sich auf Rangstufen in der Uni-Laufbahn.)

|
Ingo Althöfer
Bernstein gibt es in verschiedensten Farben, vor allem auch in braun und blau. Gauss hat mindestens zweierlei mit Bernstein zu tun. Zum einen war (natürlicher) Bernstein ein wichtiger Stoff bei den auch von Gauss betriebenen Experimenten zur Elektrizität. Zum anderen gab es (nach Gauss, aber durch ihn geprägt) in Göttingen den bekannten Mathematiker Felix Bernstein.
Zum Spielmaterial gehören neben Brett, Klötzen, Würfel auch 9 einzelne Centmünzen. Um sie herum bilden sich im Laufe des Spiels Bernstein-Klumpen. Bei der Abrechnung am Spielende wird ein Klumpen dem Spieler gutgeschrieben, dessen Farbe den grösseren Anteil am Klumpen hat. Wer holt sich mehr Klumpen? Es gibt eine Solitär-Variante, bei der es das Ziel ist, möglichst viele gute Bernstein-Klumpen auf das Brett zu zaubern, die ausserdem als Gesamt-Ensemble schön ausschauen sollen.

|
Reinhold Wittig
Die Glocken-Kurve im grossen Spielplan zeigt schematisch eine "Gauss'sche Normalverteilung".
Gespielt werden zwei Runden. In der ersten Runde legt Spieler A seine erwürfelten Klötze parallel zur Grundlinie der Kurve, Spieler B die seinen senkrecht dazu. In der zweiten Runde tauschen beide ihre Aufgaben. Klötze, die nicht mehr unter die Kurve passen, müssen beiseite gelegt werden. Wer nach beiden Runden die geringere Menge Holz beiseite gelegt hat, gewinnt.

|