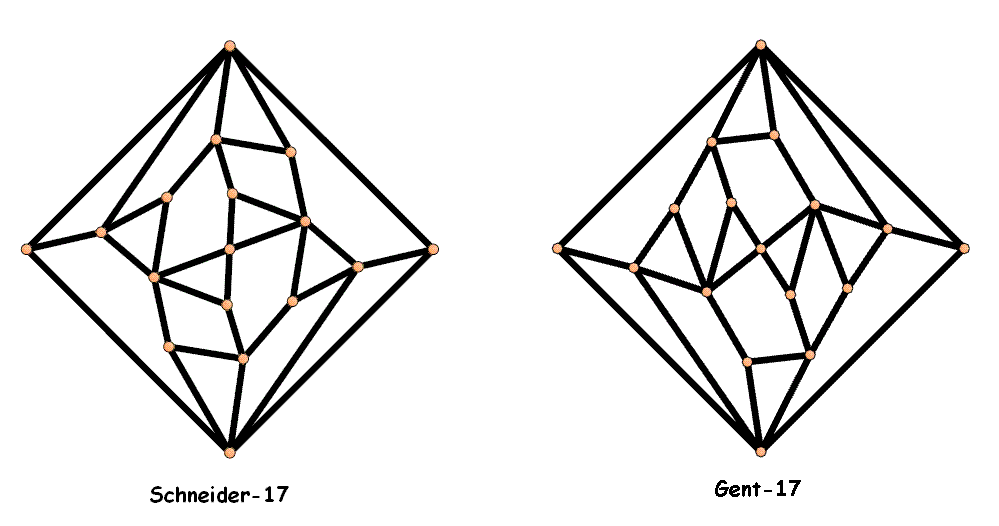Schneider von Gent
Board game, designed by Ingo Althöfer,
Copyright March 2013

"Schneider von Gent" is an asymmetric board game for two players.
The idea arose when two different alternating planar
graphs with 17 vertices and 17 faces had been found: one
("Schneider-17") by Frank Schneider back in 2008, the other one
("Ghent-17") by the group of Professor Gunnar Brinkmann at Ghent
University early in 2013.
The Ghent group also proved by complete enumeration that
these are the only alternating planar graphs with 17
vertices; and their computer runs
also showed that there do not exist
3-connected alternating planar graphs with less than 17 nodes.
As a city, Ghent in Belgium was famous for several centuries
for manufacturing and dealing with broadcloth.
And "Schneider", the family name of Frank Schneider, is German
and means "taylor". This cross relation - and the fact that
in general
planar graphs of appropriate size give nice game boards - made
me think of a corresponding board game.
"Schneider von Gent" can be played either on the Schneider-17 graph
or on the Ghent-17. At home, I have a laminated board where on one side the
Schneider-17 is given, and on the other side the Ghent-17. Depending on my mood I select this or that board.
Game parts:
The board is either a Ghent-17 or a Schneider-17, drawn as a planar
graph with a quadrangle as the outer face. A thimble, about 50 matches,
and 16 buttons.
The two players are:
(T) The taylor. Her only active piece is the thimble. The taylor
uses the matches to indicate over which edges of the graph the thimble
has moved already.
(B) Mr. Button. His pieces are the 16 buttons.
Preparation for the game:
At the beginning, in each inner face of the graph one button is
placed. (The outer face does not play a role.). A button in a face
is called free, a button on a node is called in prison.
Course of the Game
The players move in turn. Before the first normal move, Mr. Button selects
one of the nodes as the starting node for the thimble of his opponent.
Then the move order is strictly alternating, starting with the taylor
(so, T-B-T-B-T-B-...).
In each move of the taylor, the thimble walks from her current node over an open edge
to a neighboring node. It is important that this neighboring node
does not carry a button yet, and that the edge to this node does
not carry matches (or a single match), yet.
At the end of the move the edge will be marked by matches:
a short edge by a single match, a longer one
by several matches, so that it looks like a proper seam.
And now comes the reward part of the move:
If at least one of the faces next to the used edge
still has a button, the taylor is allowed to take one
such button and move it to the starting node of the
move. But: the taylor is also allowed not to take such
a button when he prefers that.
In any case: each taylor move blocks the edge over which he
has gone. The graph has 32 edges, so after at most 32 moves by
the taylor the game is over. (In practice a game will seldomly
have more than 20 pairs of moves.)
Mr. Button in each of his moves has a choice:
Either he simply does nothing. Or he moves one of his
free buttons over an edge without a seam to an empty
neighboring inner face. (To say it again: The outer face
is not part of the game.)
By his seams, the taylor step by step builds a net
which restricts the feasible moves of both Mr. Button and himself.
The End of the Game
The game ends when the taylor has no more feasible move.
Often already a few moves before the formal end it can be
recognized that the taylor will catch no more buttons.
If both players agree on this the game can be finished
immediately, and the counting be done.
The final count works as follows: For each button in prison the
taylor gets the degree of that node (= the number of edges adjacent
to that node). These values are summed up.
So, for the taylor it makes sense to "collect" prisoners on nodes
with high degrees.
Between players A and B,
two games as described above are played. In the first one, player A
is the taylor, and player B is Mr. Button. In game 2 the roles are
reversed. Total winner
is who scores more points when he is taylor. In case of a tie the player
who was taylor in the first game, is declared "small winner".
The complexity of the game is such that it can not "easily" be
solved with computer help.
See also the board game
Karl's Race.
Here are some photos of a sample game.
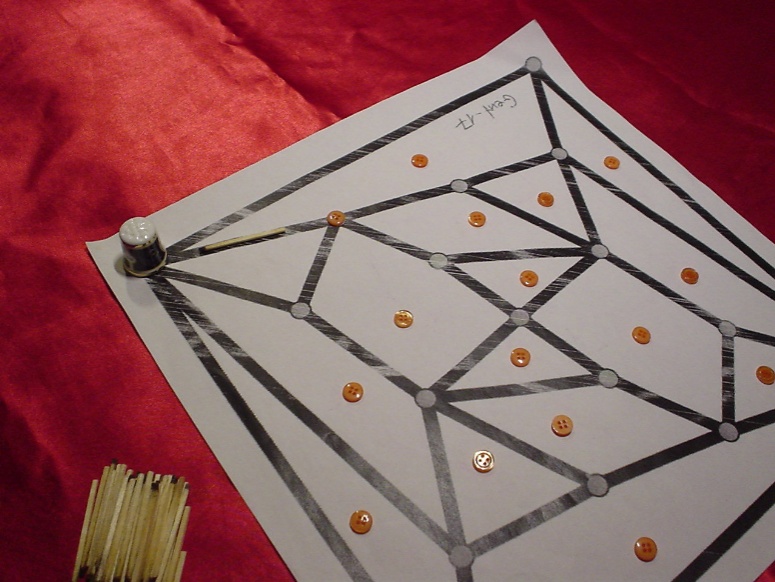
Position after the first normal move of the taylor. The match indicates
from where the thimble walked to the corner node.

Position after the first move of Mr. Button. Indeed he
has moved a button.

Position after move 8 of Mr. Button.

Position after move 13 of the taylor. Now the taylor has no
more feasible moves. So the game ends, and counting is done.
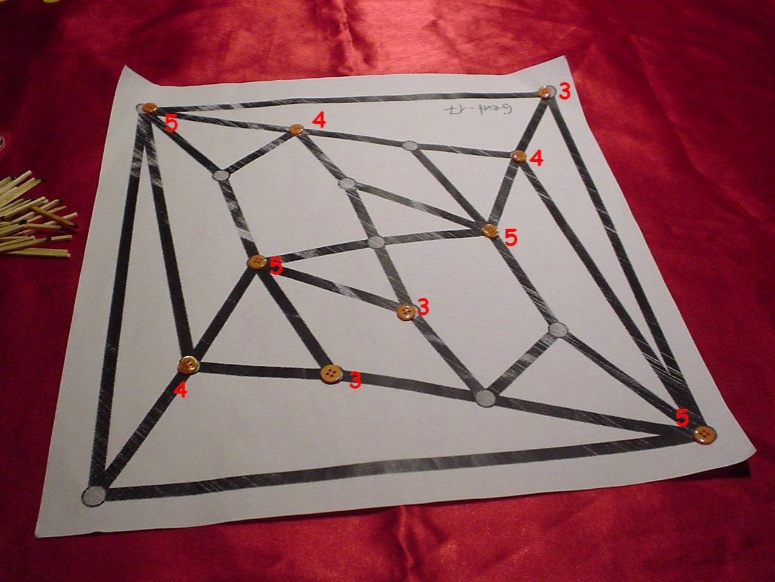
Here the buttons in prison are shown together with the resulting
points for the taylor. In total, her score is 41.
Zur Spielregel auf deutsch
Back to the event site of 3-Hirn-Verlag